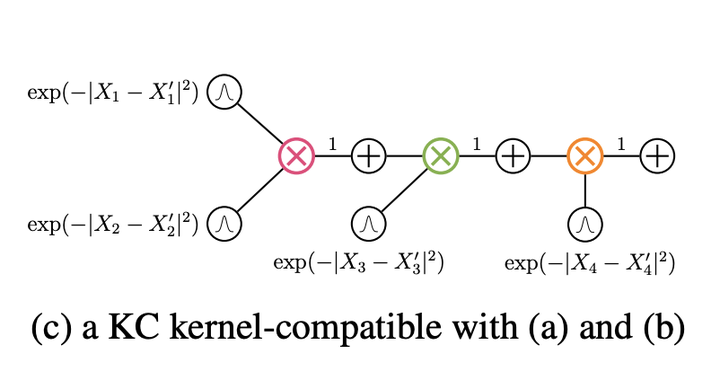
 An Example Kernel Circuit
An Example Kernel CircuitAbstract
Computing the expectation of kernel functions is a ubiquitous task in machine learning, with applications from classical support vector machines to exploiting kernel embeddings of distributions in probabilistic modeling, statistical inference, causal discovery, and deep learning. In all these scenarios, we tend to resort to Monte Carlo estimates as expectations of kernels are intractable in general. In this work, we characterize the conditions under which we can compute expected kernels exactly and efficiently, by leveraging recent advances in probabilistic circuit representations. We first construct a circuit representation for kernels and propose an approach to such tractable computation. We then demonstrate possible advancements for kernel embedding frameworks by exploiting tractable expected kernels to derive new algorithms for two challenging scenarios: 1) reasoning under missing data with kernel support vector regressors; 2) devising a collapsed black-box importance sampling scheme. Finally, we empirically evaluate both algorithms and show that they outperform standard baselines on a variety of datasets.