Probabilistic Inference with Algebraic Constraints: Theoretical Limits and Practical Approximations

Abstract

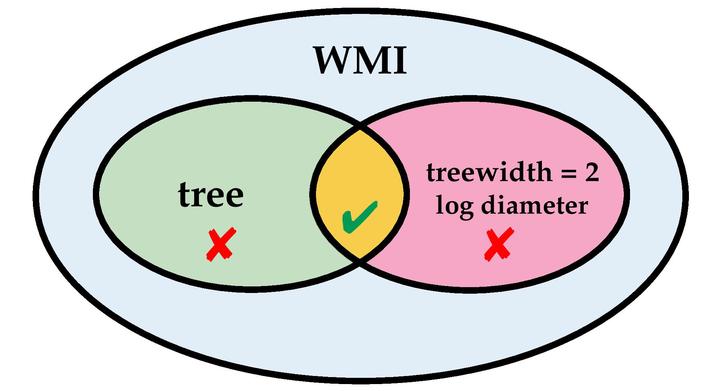
Weighted model integration (WMI) is a framework to perform advanced probabilistic inference in hybrid domains, i.e., on distributions over mixed continuous-discrete random variables and in the presence of complex logical and arithmetic constraints. In this work, we advance the WMI framework on both the theoretical and algorithmic side. First, we trace the boundaries of tractability for WMI inference in terms of two key properties of a WMI problem’s dependency structure, sparsity and diameter. We prove that exact inference is only efficient if that structure is tree-shaped with logarithmic diameter. While this result deepens our theoretical understanding of WMI it hinders the practical applicability of exact WMI solvers to large problems. To overcome this, we propose the first approximate WMI solver that does not resort to sampling, but performs exact inference on an approximate model. Our solution iteratively performs message passing in a relaxed problem structure to recover lost dependencies. As our experiments show, it scales to problems that are out of the reach of exact WMI solvers while delivering accurate approximations.

Zhe Zeng

Assistant Professor

I do research in probabilistic ML and neurosymbolic AI to enable and support decision-making in the real world in the presence of probabilistic uncertainty and symbolic knowledge, where the symbolic knowledge can be graph structures and logical, arithmetic, and physical constraints.